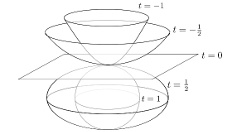
Consider a hyperboloid, a plane and a round sphere as in the figure below. Although the geometry of these three objects is fundamentally different, it is possible to transition  between them. Flattening the hyperboloid gives the plane. Alternatively, inflating a sphere to a very large radius makes it locally look like a plane. Both of these are examples of a geometric transition: a continuous path of geometric structures that changes the geometric type in the limit, producing a limit of geometries. Geometric transitions arise in the seminal program for 3-dimensional manifolds of Thurston, and deform general relativity into special relativity, or quantum mechanics into Newtonian mechanics.

The above-mentioned geometries are modelled over the usual number system, the real numbers. An alternative is the $p$-adic numbers, where $p$ is a prime number and the digits used are from 0 to $p−1$. The $p$-adic numbers and $p$-adic geometries are at the core of the 2018 Fields medalist Peter Scholze's groundbreaking work, and fundamental tools in number theory, algebraic geometry, representation theory, arithmetic dynamics, and cryptography. So far limits of geometries over the $p$-adic numbers have been studied very little, this direction of research is not yet explored.

"The objective of my Villum project is to answer the following fundamental questions for many of the possible $p$-adic geometries: Given a family of geometries, can one compute all its possible limits of geometries? Can one provide precise geometric transitions towards those limits? This is an exciting opportunity for me to combine my unique background in $p$-adic metric geometry, buildings and Chabauty topology with my knowledge of symmetric spaces and limits of geometries over the reals, and to conduct a type of research on limits of geometries that differs from the research that has been done before. My scientific key idea is to use purely metric geometric techniques, an approach that has not been employed so far, and to provide a much deeper understanding of the $p$-adic geometries and the interconnection between them.

I am confident my project's results will find applications to the $p$-adic Langlands program, a collection of deep interconnected conjectures and theorems relating number theory and geometry."

– Corina-Gabriela Ciobotaru

The Villum Young Investigator grant (DKK 5,997,248) funds a PhD student and a postdoc.

VILLUM FONDEN aim to support early career researchers with ambitions of creating their own, independent research identity, and with the potential to significantly contribute to research in technical and natural sciences at a Danish research institution. With the Villum Young Investigator Programme they encourage Danish universities to support and recruit Danish as well as international researcher talents.

• Villum Young Investigators 2023